Olá, queridos alunos! Prontos para a nossa aula de número 16? Hoje vamos começar a estudar as Equações Irracionais. Vamos lá!
O estudo de equações consiste em encontrarmos um valor para a incógnita da equação de modo que esta satisfaça aquela condição de igualdade.
A equação irracional é aquela na qual a incógnita está em um radicando, ou seja, dentro da raiz.
Para resolver uma equação irracional a radiciação deve ser eliminada, transformando-a em uma equação racional mais simples para encontrar o valor da variável.
Exemplo 1:
1º passo: isole o radical no primeiro membro da equação.
2º passo: eleve ambos os membros da equação ao número que corresponde ao índice do radical.
Por se tratar de uma raiz quadrada, deve-se elevar os dois membros ao quadrado e, com isso, elimina-se a raiz.
3º passo: encontre o valor de x resolvendo a equação.
4º passo: verifique se a solução é verdadeira.
4º passo: verifique se a solução é verdadeira.
Para a equação irracional, o valor de x é – 2.
Exemplo 2:
1º passo: elevar ambos os membros da equação ao quadrado.
2º passo: resolva a equação.
4º passo: verificar qual a solução verdadeira para a equação.
Para a equação irracional, o valor de x é 3.
Para a equação irracional, o valor x = – 1 não é uma solução verdadeira.
Para que você consiga entender melhor, assista com muita atenção aos vídeos abaixo:
:: Atividade
1) Resolva as equações irracionais:
a) 
b)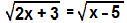 
Clique na imagem para enviar sua tarefa desta aula:
Clique na imagem para confirmar sua presença nesta aula:
Importante: Todas as quintas-feiras estarei online de 14:00 às 15:00 para tirar as dúvidas de vocês ao vivo no chat do blog!
"E lembrem-se de sempre lavar bem as mãos e evitar sair de casa! Somente juntos, com a colaboração de todos, conseguiremos superar esta situação!"
E.M.A.C. Rodrigues Alves
0 Comentários