Olá, queridos alunos! Prontos para a nossa aula de número 9? Hoje vamos aprender Plano Cartesiano. Vamos lá!
O plano cartesiano é um sistema de coordenadas desenvolvido por René Descartes. Esse sistema de coordenadas é formado por duas retas perpendiculares, chamadas de eixos cartesianos. Esses eixos determinam um único plano, assim, é possível determinar a localização no sistema de coordenadas de todo os pontos e, consequentemente, de qualquer objeto formado por esses pontos que estejam nesse plano.
Desse modo, perceba que é possível representar pontos ou objetos utilizando somente suas coordenadas, isto é, não é necessário construir um desenho de um objeto, basta somente expressar suas coordenadas.
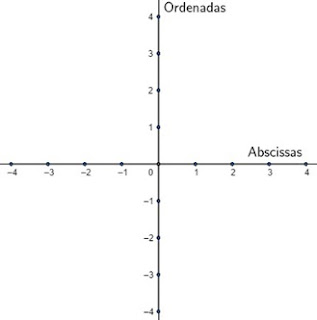
O plano cartesiano é formado por duas retas reais em que o ângulo entre elas é de 90°, ou seja, elas são perpendiculares. Essas retas são chamadas de eixos. Assim, há o eixo horizontal, que é chamado de eixo das abscissas, e o eixo vertical, que é o eixo das ordenadas.
Perceba que as retas perpendiculares dividem o plano em quatro regiões, que são chamadas de quadrantes.
Vamos representar os quadrantes no sentido anti-horário. Veja:
A relação dos quadrantes é dada por:
• Quadrante I: positivo, positivo; (+,+)
• Quadrante II: negativo, positivo; ( –, +)
• Quadrante III: negativo, negativo; ( –, –)
• Quadrante IV: positivo, negativo. ( +, –)
Obs: Note que o ponto em que os eixos se encontram é chamado de “origem” e corresponde ao par ordenado (0, 0).
:: Ponto em um plano cartesiano
Um ponto qualquer do plano cartesiano é indicado a partir de suas coordenadas, que são representadas por um par ordenado, ou seja, um ponto é formado por um conjunto de dois números que possui uma ordem a ser seguida (ordenado). A notação do par ordenado ou ponto P é:
P (x, y)
x → à Abscissa
y → à Ordenada
Assim, para localizar um ponto, basta marcar o valor no eixo das abscissas e, em seguida, o valor no eixo das ordenadas. Depois trace uma reta perpendicular aos pontos x e y encontrados. O local onde essas retas perpendiculares se encontram é onde ponto P está.
Obs:
1. De um modo geral, sendo x e y dois números racionais quaisquer, temos: (x,y) ≠ (y,x)
( 1, – 3) ≠ ( – 3 , 1)
2. Dois pares ordenados (x, y) e (r, s) são iguais somente se x = r e y = s.
Exemplo:
1) Marque os pontos A (2, 3), B (-2,5), C (-3, -2) e D (1, -4) no plano cartesiano.
:: Exercícios
1. Identifique a abscissa e a ordenada dos pontos abaixo.
A(3,-5) abscissa________ ordenada__________
B(-1,0) abscissa________ ordenada__________
C(-3,5;-2) abscissa________ ordenada_________
D(0,-1) abscissa________ ordenada___________
E(-5,3) abscissa________ ordenada___________
F(0,0) abscissa________ ordenada___________
G(-2; -0,5) abscissa________ ordenada__________
2. Localize os pontos no plano cartesiano:
(a) A = ( 0 , 4 )
(b) B = ( - 4 , 5 )
(c) C = ( 3 , - 4 )
(d) D = ( 2 , 2 )
(e) E = ( 0 , 0 )
3. Em quais quadrantes estão localizados os pontos:
a) (-2, -4)
b) (3, 1)
c) (0, 6)
d) (8, -7)
e) (9, -3)
4. No plano cartesiano abaixo, escreva os pares ordenados de cada ponto:
5. Quais são as coordenadas que estão indicando a cidade do Estado:
a) do Acre
b) do Mato Grosso do Sul
c) do Rio Grande do Norte
d) de Minas Gerais
e) do Amazonas
f) do Espirito Santo
g) de Roraima
h) do Rio Grande do Sul
i) do Pará
j) de Mato Grosso
k) de Pernambuco
l) de São Paulo
6) Faça os exercícios da apostila página 118
7) Agora, resolva também os exercícios do formulário, clicando na imagem abaixo:
Importante: Todas as quintas-feiras estarei online de 14:00 às 15:00 para tirar as dúvidas de vocês ao vivo no chat do blog!
"E lembrem-se de sempre lavar bem as mãos e evitar sair de casa! Somente juntos, com a colaboração de todos, conseguiremos superar esta situação!"
E.M.A.C. Rodrigues Alves





















0 Comentários