Matemática - 9º ano - Aula 6 - Revisão de Conteúdos

Olá, queridos alunos! Prontos para a nossa aula de número 6? Chegamos ao final do conteúdo do 1° Bimestre, por isso é hora da REVISÃO!

Vamos dividir a revisão por partes, começando pelas primeiras aulas:

:: Teorema de Tales

Teorema de Tales é como ficou conhecida a propriedade matemática que relaciona as medidas dos segmentos de reta formados por um feixe de retas paralelas cortado por retas transversais. Antes de falar do teorema em si, é bom lembrar o conceito de feixe de retas paralelas, retas transversais e uma de suas propriedades

Duas ou mais retas são paralelas quando elas não possuem nenhum ponto em comum. Quando destacamos três ou mais retas paralelas em um plano, dizemos que elas formam um feixe de retas paralelas. As retas transversais são aquelas que “cortam” as retas paralelas.

Para compreender melhor o teorema enunciado, observe a imagem a seguir:

O que o teorema de Tales garante a respeito dos segmentos formados sobre as retas transversais é a seguinte igualdade:

Exemplo:

No feixe de retas paralelas a seguir, vamos determinar a medida do segmento NM.

Solução:

Seja x o comprimento do segmento NM, vamos mostrar a proporcionalidade entre os segmentos e utilizar a propriedade fundamental das proporções para resolver a equação:

:: Semelhança de Triângulos

Dois triângulos são semelhantes quando possuem os três ângulos ordenadamente congruentes (iguais) e os lados correspondentes proporcionais. Usamos o símbolo ~ para indicar que dois triângulos são semelhantes.

Para saber quais são os lados proporcionais, primeiro devemos identificar os ângulos de mesma medida. Os lados homólogos (correspondentes) serão os lados opostos a esses ângulos.

:: Casos de Semelhança

Para identificar se dois triângulos são semelhantes, basta verificar alguns elementos.

1º Caso de semelhança: Ângulo-Ângulo (AA)

Sempre que dois triângulos possuírem dois ângulos correspondentes congruentes, eles já serão completamente semelhantes. Perceba que, se dois triângulos possuem dois ângulos congruentes, eles também apresentam o terceiro ângulo congruente. Isso é garantido pela soma dos ângulos internos dos triângulos que sempre será igual a 180°.

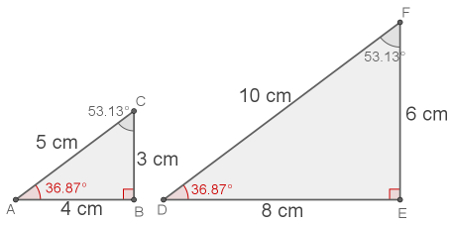
O exemplo seguinte mostra em vermelho dois ângulos congruentes de dois triângulos distintos. O restante das medidas foi colocado em cinza apenas para perceber-se a semelhança entre os triângulos.

Observe que os lados correspondentes desses dois triângulos são proporcionais e que os ângulos que sobraram, destacados na cor cinza, são iguais.

2º Caso de semelhança: Lado-Lado-Lado (LLL)

Sempre que dois triângulos possuírem três lados correspondentes proporcionais, então eles serão semelhantes. Em outras palavras, triângulos que possuem três lados proporcionais sempre apresentam os ângulos correspondentes iguais.

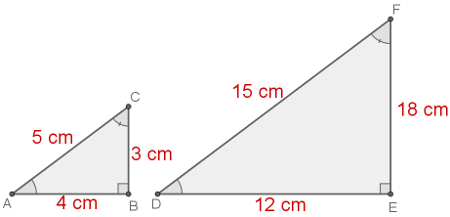
O exemplo a seguir mostra dois triângulos semelhantes, pois eles possuem as medidas de seus três lados proporcionais. Em cinza, estão as medidas dos ângulos desses triângulos.

3º Caso de semelhança: Lado-Ângulo-Lado (LAL)

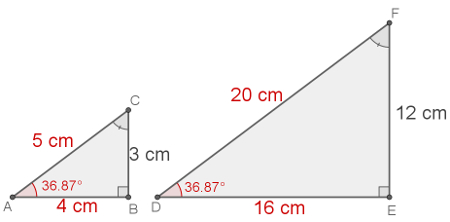
Se dois triângulos distintos possuem dois lados proporcionais e o ângulo entre esses lados é congruente, então esses dois triângulos são semelhantes. Na imagem a seguir, veja um exemplo de triângulos com dois lados proporcionais e o ângulo entre eles congruente. Colocamos no exemplo o restante das medidas do triângulo em cinza para evidenciar a semelhança entre eles.

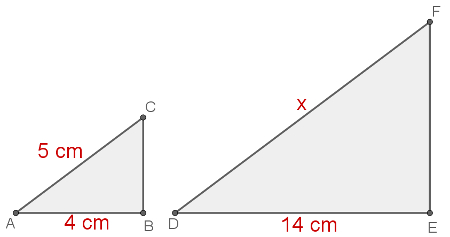
Exemplo: Os dois triângulos a seguir são semelhantes. Determine a medida do segmento DF.

Como dois triângulos semelhantes possuem lados correspondentes proporcionais, para descobrir a medida de x, basta montar a proporção:

5/x = 4/14 (fazemos o "cruz credo")
4x = 5·14
4x = 70
x = 70 : 4
x = 17,5 cm

:: Exercícios

Agora, resolva os exercícios, clicando na imagem abaixo:

Importante: Todas as quintas-feiras estarei online de 14:00 às 15:00 para tirar as dúvidas de vocês ao vivo no chat do blog!

Bons estudos! Professor Marcos

"E lembrem-se de sempre lavar bem as mãos e evitar sair de casa! Somente juntos, com a colaboração de todos, conseguiremos superar esta situação!"

E.M.A.C. Rodrigues Alves