Olá, queridos alunos! Prontos para a nossa aula de número 10? Hoje vamos estudar o Discriminante Delta. Vamos lá!
:: O discriminante (Δ)
A fórmula resolutiva para equações completas e incompletas do 2º grau é a fórmula de Bháskara, dada por:
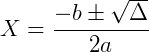
Sendo:
Δ = b² − 4.a.c
O discriminante, representado pela letra grega Δ (lê-se “delta”) corresponde ao radicando da fórmula resolutiva.
A representação geral de uma equação de 2º grau é:
ax² + bx + c = 0, com a ≠ 0.
:: Particularidades de Δ
Algumas peculiaridades do discriminante merecem atenção. Veja cada uma delas:
1. Δ = 0. Quando o discriminante é igual à zero a equação de 2º grau apresenta duas raízes iguais.
Ex.: Resolva a equação x² – 6x + 9 = 0.
1º passo: Separando os coeficientes
a = 1, b = – 6 e c = 9
2º Passo: Calculando o valor do discriminante
Δ = b² – 4ac
Δ = (– 6)² – 4.1.9
Δ = 36 – 36
Δ = 0
3º Passo: Determinando os valores de x:
2. Δ > 0. Quando o valor do discriminante é maior que zero, a equação apresenta duas raízes diferentes.
Ex.: Resolva a equação x² + 3x – 4 = 0.
1º passo: Separando os coeficientes
a = 1, b = 3 e c = – 4
2º Passo: Calculando o valor do discriminante
Δ = b² – 4ac
Δ = (3)² – 4.1.(– 4)
Δ = 9 – 16
Δ = 25
3º Passo: Determinando os valores de x:
3. Δ < 0. Quando o discriminante é menor que zero, não existem raízes reais (em R).
Ex.: Determine o conjunto solução da equação quadrática x² + 5x + 7 = 0.
1º passo: Separando os coeficientes
a = 1, b = 5 e c = 7
2º Passo: Calculando o valor do discriminante
Δ = b² – 4ac
Δ = 5² – 4.1.(7)
Δ = 25 – 28
Δ = – 3
3º Passo: Determinando os valores de x:
Portanto, o conjunto solução desta equação é: S=∅.
Para que você possa compreender melhor, assista com muita atenção ao vídeo abaixo:
:: Exercícios
1) Resolva apenas o discriminante (Δ) e analise quantas raízes terá cada uma das equações abaixo
a) x² - 8x + 7 = 0
b) x² - 10x + 25 = 0
c) x² - 5x + 4 = 0
d) x² + 10x + 21 = 0
e) x² - 2x + 9 = 0
f) x² + 4x + 4 = 0
g) x² + 6x + 15 = 0
2) Agora, resolva por completo as equações utilizando a fórmula de Bháskara e determine o valor de suas raízes.
2) Agora, resolva por completo as equações utilizando a fórmula de Bháskara e determine o valor de suas raízes.
a) x² - 9x + 18 = 0
b) x² - 8x + 16 = 0
c) x² - 5x + 14 = 0
d) x² + 12x + 36 = 0
e) x² - 7x + 12 = 0
Clique na imagem para enviar sua tarefa desta aula:
Clique na imagem para confirmar sua presença nesta aula:
:: Referências
Importante: Todas as quintas-feiras estarei online de 14:00 às 15:00 para tirar as dúvidas de vocês ao vivo no chat do blog!
"E lembrem-se de sempre lavar bem as mãos e evitar sair de casa! Somente juntos, com a colaboração de todos, conseguiremos superar esta situação!"
E.M.A.C. Rodrigues Alves



















0 Comentários