Olá, queridos alunos! Prontos para a nossa aula de número 5? Desta vez vamos revisar o cálculo de Porcentagem e Probabilidades.
:: PORCENTAGEM
- Definição:
Porcentagem pode ser definida como a centésima parte de uma grandeza, ou o cálculo baseado em 100 unidades.
É visto com frequência as pessoas ou o próprio mercado usar expressões de acréscimo ou redução nos preços de produtos ou serviços.
Alguns exemplos:
– O Leite teve um aumento de 25% Quer dizer que de cada R$ 100,00 teve um acréscimo de R$ 25,00.
– O cliente teve um desconto de 15% na compra de uma calça jeans Quer dizer que em cada R$ 100,00 a loja deu um desconto de R$ 15,00.
– Dos funcionários que trabalham na empresa, 75% são dedicados. Significa que de cada 100 funcionários, 75 são dedicados ao trabalho ou a empresa.
Para ajudar você a compreender melhor não deixe de assistir aos vídeos abaixo:
:: Conceitos Básicos de Probabilidade
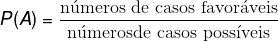
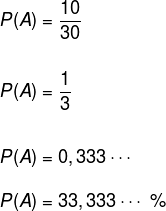
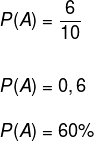
Bons estudos! Professor Marcos
Para ajudar você a compreender melhor não deixe de assistir aos vídeos abaixo:
:: Conceitos Básicos de Probabilidade
Experimento aleatório: Experimentos aleatórios são aqueles que, quando repetidos por diversas vezes e mantendo-se os processos de execução, resultam em resultados improváveis. Por exemplo, quando lançamos uma moeda dez vezes seguidas, os resultados são improváveis, visto que, em cada lançamento, pode aparecer a face cara ou a face coroa.
Espaço amostral: Vamos chamar de espaço amostral o conjunto de todos os possíveis resultados de determinado fenômeno ou do experimento aleatório.
Espaço amostral: Vamos chamar de espaço amostral o conjunto de todos os possíveis resultados de determinado fenômeno ou do experimento aleatório.
Exemplos:
a) Ao lançar uma moeda, os possíveis resultados são cara ou coroa, logo o espaço amostral é:
E = {cara, coroa}
b) No lançamento de um dado honesto, os possíveis resultados são as seis faces do dados, logo:
E = {1, 2, 3, 4, 5, 6}
Evento: Um evento é todo subconjunto de um espaço amostral.
Exemplos:
Considere o espaço amostral do lançamento de um dado, logo E = {1,2,3,4,5,6}. Os casos a seguir são exemplos de eventos:
a) Evento no qual as faces são maiores que 3. Vamos denotar tal evento por A, logo:
A = {4, 5, 6}
b) Evento no qual as faces são números ímpares. Nesse caso, vamos denotar tal evento por B, assim:
B = {1, 3, 5}
:: Fórmula e Cálculo da Probabilidade
A probabilidade de acontecer determinado evento A, representado por P(A), é a divisão entre o número de casos favoráveis e o número de casos possíveis. Podemos representar, então, a chance de ocorrer o evento A por:
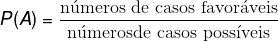
Exemplo
a) Vamos determinar a probabilidade de tirarmos uma bola branca em uma urna com 10 bolas brancas e 20 bolas vermelhas.
Solução:
Para isso, vamos inicialmente determinar o número de casos favoráveis e o número de casos possíveis.
Casos favoráveis → 10 (bolas brancas)
Casos possíveis → 10 + 20 (bolas brancas + bolas vermelhas)
Veja que os casos favoráveis são os casos que nos interessam – nesse caso, a quantidade de bolas brancas – e casos possíveis representam o total de elementos do espaço amostral. Vamos chamar de A o evento em questão, assim:
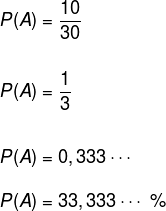
b) Uma letra é escolhida ao acaso dentre as que formam a palavra PERNAMBUCO. Qual a probabilidade de ser uma consoante?
Solução:
Observe que o total de letras na palavra PERNAMBUCO é igual a 10. O caso favorável nesse problema é a quantidade de consoantes, que são 6. Logo, a probabilidade de escolhermos uma consoante é de:
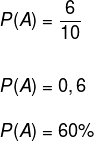
(Retirado de: https://escolakids.uol.com.br/matematica/probabilidade.htm)
E aí, conseguiu compreender o conceito das probabilidades? Simples, não? Mas para que você consiga entender ainda melhor, assista ao vídeo abaixo:
Importante: Todas as quintas-feiras estarei online de 14:00 às 15:00 para tirar as dúvidas de vocês ao vivo no chat do blog!
"E lembrem-se de sempre lavar bem as mãos e evitar sair de casa! Somente juntos, com a colaboração de todos, conseguiremos superar esta situação!"
E.M.A.C. Rodrigues Alves


















0 Comentários