Olá, queridos alunos e alunas! Como vocês estão nessa quarentena? Todos se cuidando e seguindo as orientações de ficar em casa? Só juntos conseguiremos superar esta situação!
Devido ao ponto facultativo de Páscoa, não houve conteúdo novo na última semana, portanto essa será nossa aula 3.
:: Semelhança de Triângulos
Dois triângulos são semelhantes quando possuem os três ângulos ordenadamente congruentes (iguais) e os lados correspondentes proporcionais. Usamos o símbolo ~ para indicar que dois triângulos são semelhantes.
Para saber quais são os lados proporcionais, primeiro devemos identificar os ângulos de mesma medida. Os lados homólogos (correspondentes) serão os lados opostos a esses ângulos.
:: Razão de Proporcionalidade
Como nos triângulos semelhantes os lados homólogos são proporcionais, o resultado da divisão desses lados será um valor constante. Esse valor é chamado de razão de proporcionalidade.
Considere os triângulos ABC e EFG semelhantes, representados na figura abaixo:
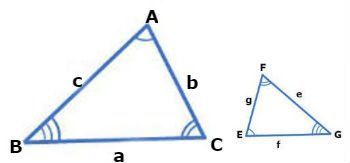
Os lados a e e, b e g, c e f são homólogos.
:: Casos de Semelhança
Para identificar se dois triângulos são semelhantes, basta verificar alguns elementos.
1º Caso de semelhança: Ângulo-Ângulo (AA)
Sempre que dois triângulos possuírem dois ângulos correspondentes congruentes, eles já serão completamente semelhantes. Perceba que, se dois triângulos possuem dois ângulos congruentes, eles também apresentam o terceiro ângulo congruente. Isso é garantido pela soma dos ângulos internos dos triângulos que sempre será igual a 180°.
O exemplo seguinte mostra em vermelho dois ângulos congruentes de dois triângulos distintos. O restante das medidas foi colocado em cinza apenas para perceber-se a semelhança entre os triângulos.
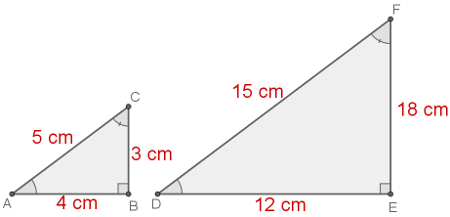
2º Caso de semelhança: Lado-Lado-Lado (LLL)
Sempre que dois triângulos possuírem três lados correspondentes proporcionais, então eles serão semelhantes. Em outras palavras, triângulos que possuem três lados proporcionais sempre apresentam os ângulos correspondentes iguais.
O exemplo a seguir mostra dois triângulos semelhantes, pois eles possuem as medidas de seus três lados proporcionais. Em cinza, estão as medidas dos ângulos desses triângulos.
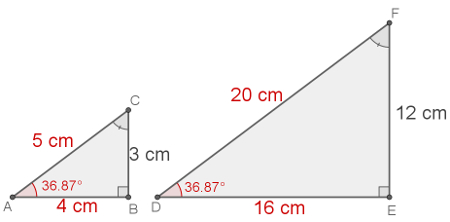
Se dois triângulos distintos possuem dois lados proporcionais e o ângulo entre esses lados é congruente, então esses dois triângulos são semelhantes. Na imagem a seguir, veja um exemplo de triângulos com dois lados proporcionais e o ângulo entre eles congruente. Colocamos no exemplo o restante das medidas do triângulo em cinza para evidenciar a semelhança entre eles.
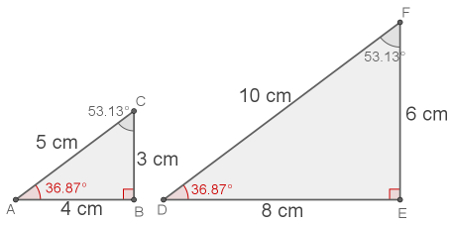
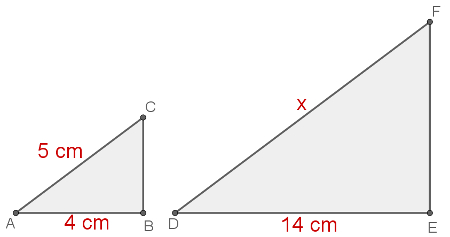
Exemplo: Os dois triângulos a seguir são semelhantes. Determine a medida do segmento DF.
5/x = 4/14 (fazemos o "cruz credo")
4x = 5·14
4x = 70
x = 70 : 4
x = 17,5 cm
4x = 5·14
4x = 70
x = 70 : 4
x = 17,5 cm
:: Teorema Fundamental da semelhança
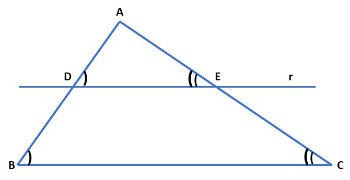
Quando uma reta paralela a um lado de um triângulo intersecta (corta) os outros dois lados em pontos distintos, forma um triângulo que é semelhante ao primeiro.
Na figura abaixo, representamos o triângulo ABC e a reta r paralela ao lado 
.
.
são congruentes, assim como os ângulos 
, pois a reta r é paralela ao lado 
. Assim, pelo critério AA, os triângulos ABC e ADE são semelhantes.
Ainda ficou com dúvidas? Então assista o vídeo abaixo com uma outra forma de explicação da semelhança de triângulos:
:: Exercícios
1) Qual o valor de x nos triângulos a seguir?
a) 60 cm
b) 49 cm
c) 50 cm
d) 54 cm
e) 20 cm
2) Na imagem a seguir, é possível perceber dois triângulos que compartilham parte de dois lados. Sabendo que os segmentos BA e DE são paralelos, qual a medida de x?
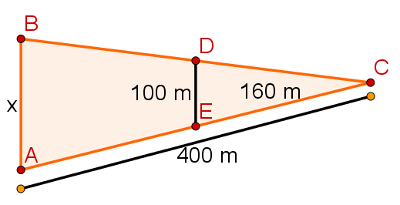
a) 210 m
b) 220 m
c) 230 m
d) 240 m
e) 250 m
3) Para descobrir a altura de um prédio, Luiz mediu a sombra do edifício e, em seguida, mediu sua própria sombra. A sombra do prédio media 7 metros, e a de Luiz, que tem 1,6 metros de altura, media 0,2 metros. Qual a altura desse prédio?
a) 50 metros
b) 56 metros
c) 60 metros
d) 66 metros
e) 70 metros
4) Observe os triângulos da imagem a seguir e assinale a alternativa correta.
a) Os triângulos são semelhantes, pois possuem o mesmo formato. Essa é a única maneira de descobrir se duas figuras geométricas são semelhantes.
b) Os triângulos não são semelhantes, pois não existe caso de semelhança para quando se conhece apenas um lado e um ângulo de dois triângulos.
c) Os triângulos são congruentes pelo caso LLL.
d) Os triângulos são semelhantes pelo caso AA (Ângulo – Ângulo).
5) (Unesp) A sombra de um prédio, em um terreno plano, em uma determinada hora do dia, mede 15 m. Nesse mesmo instante, próximo ao prédio, a sombra de um poste de altura 5 m mede 3 m. A altura do prédio, em metros, é:
a) 25
b) 29
c) 30
d) 45
e) 75
6) Qual é a medida do segmento BC?
a) 1
b) 2
c) 3
d) 4
e) 5
7) Numa cidade do interior, à noite, surgiu um objeto voador não identificado, em forma de disco, que estacionou a 50 m do solo, aproximadamente. Um helicóptero do exército, situado a aproximadamente 30 m acima do objeto, iluminou-o com um holofote, conforme mostra a figura anterior. Sendo assim, pode-se afirmar que o raio do disco mede, em m, aproximadamente:
a) 3,0
b) 3,5
c) 4,0
d) 4,5
e) 5,0
:: Referências:
https://brasilescola.uol.com.br/matematica/semelhanca-triangulos.htm
https://www.todamateria.com.br/semelhanca-de-triangulos/
https://exercicios.mundoeducacao.bol.uol.com.br/exercicios-matematica/exercicios-sobre-semelhanca-triangulos.htm
:: Referências:
https://brasilescola.uol.com.br/matematica/semelhanca-triangulos.htm
https://www.todamateria.com.br/semelhanca-de-triangulos/
https://exercicios.mundoeducacao.bol.uol.com.br/exercicios-matematica/exercicios-sobre-semelhanca-triangulos.htm
Importante: Todas as quintas-feiras estarei online de 14:00 às 15:00 para tirar as dúvidas de vocês ao vivo no chat do blog!
Bons estudos! Professor Marcos
"E lembrem-se de sempre lavar bem as mãos e evitar sair de casa! Somente juntos, com a colaboração de todos, conseguiremos superar esta situação!"
E.M.A.C. Rodrigues Alves
0 Comentários