Olá, queridos alunos! Vínhamos estudando em nossas aulas Potenciação, Radiciação e Notação Científica. Vamos relembrar esses conteúdos:
:: Potenciação
Primeiro, vamos relembrar algumas propriedades básicas:
- Todo número elevado ao expoente 1 é igual a ele mesmo.Exemplos:
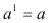

- Todo número elevado ao expoente zero é igual a 1.Exemplos:
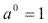

- Toda potência da base 1 é igual a 1.Exemplos:
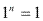

- Toda potência de 10 é igual ao numeral formado pelo algarismo 1 seguido de tantos zeros quantas forem as unidades do expoente.Exemplos:
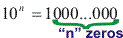
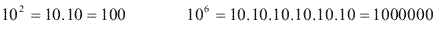
- O expoente negativo significa que ocorre a troca de lugar entre o numerador o denominador.Exemplos:
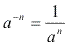

:: Produto de potências de mesma base
Considere o produto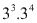 . Observe que:
. Observe que: 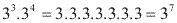
Considere o produto
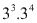 . Observe que:
. Observe que: 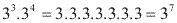
Assim:
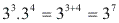
Podemos concluir então que: Multiplicando potências de mesma base, devemos conservar a base e somar os expoentes.
Assim:
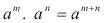
:: Divisão de potências de mesma base
Considere o quociente 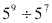 . Observe que:
. Observe que: 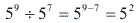
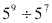 . Observe que:
. Observe que: 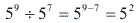
Podemos concluir então que: Para dividir potências de mesma base, não-nula, devemos
conservar a base e subtrair os expoentes.
conservar a base e subtrair os expoentes.
Assim:
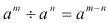
:: Potência da potência
Considere a potência 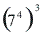 . Observe que:
. Observe que: 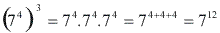
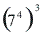 . Observe que:
. Observe que: 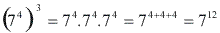
Assim: 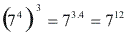
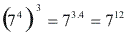
Podemos concluir então que: Para elevar uma potência a um novo expoente, devemos
conservar a base e multiplicar os expoentes.
Assim:
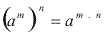
Assista aos vídeos:
:: Radiciação
Já sabemos que 6² = 36. Aprenderemos agora a operaçao que nos permite determinar qual o número que elevado ao quadrado equivale a 36 (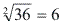 ), pois 6 elevado ao quadrado é 36. Essa operação é a inversa da potenciação e denomina-se radiciação.
), pois 6 elevado ao quadrado é 36. Essa operação é a inversa da potenciação e denomina-se radiciação.
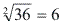 ), pois 6 elevado ao quadrado é 36. Essa operação é a inversa da potenciação e denomina-se radiciação.
), pois 6 elevado ao quadrado é 36. Essa operação é a inversa da potenciação e denomina-se radiciação.
Outros exemplos:
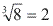 , pois 2³ = 8.
, pois 2³ = 8.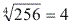 , pois
, pois 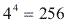 .
.
Sendo assim:
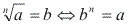
Notação:
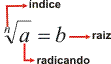
Na indicação de raiz quadrada, podemos omitir o índice 2. Por exemplo, 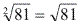 .
.
:: Simplificação de radicais
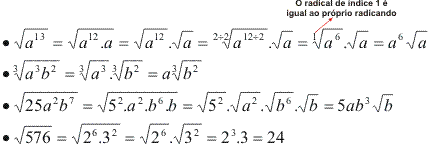
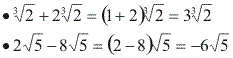
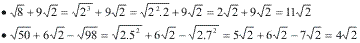
Assista aos vídeos:
:: Exercícios:
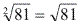 .
.:: Simplificação de radicais
Confira a seguir alguns exemplos de simplificação de radicais:
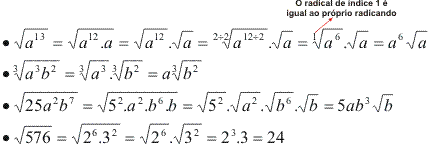
:: Adição e subtração de radicais
1º caso: Radicais semelhantes
Fazemos como na redução de termos semelhantes de uma soma algébrica. Exemplos:
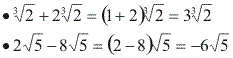
2º caso: Radicais semelhantes após simplificação
Depois de obter radicais semelhantes, procedemos como no 1º caso.
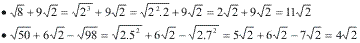
Assista aos vídeos:
:: Notação Científica
A notação científica é uma forma de escrever números usando potência de 10. É utilizada para reduzir a escrita de números que apresentam muitos algarismos.
Números muito pequenos ou muito grandes são frequentemente encontrados nas ciências em geral e escrever em notação científica facilita fazer comparações e cálculos.
Um número em notação científica apresenta o seguinte formato:
N . 10n
Sendo,
N um número real igual ou maior que 1 e menor que 10;
n um número inteiro.
Exemplos
a) 6 590 000 000 000 000 = 6,59 . 10 15
b) 0, 000000000016 = 1,6 . 10 - 11
Assista ao vídeo:
:: Exercícios:
1 - Calcule as seguintes potências:
a) (– 3 )³ = b) 12² = c) 47¹ = d) ( – 2) 5 =
e) ( – 1 ) 13 = f) 4 – 3 =
2 - Reduza
a uma só potência, usando as propriedades:
a) 6 23 • 6 4
= b) 5 – 13 : 5 – 7 = c) (7 – 3 )8 =
d) ( 17 0)3 = e) 7 23 :7 4
• 7 9 = f) ( – 2 ) 17 • ( – 2 )
– 9 : ( – 2 )¹ =
3 - Não parece, mas o olho humano tem quase o tamanho de uma bola de pingue-pongue. É uma sofisticada câmara capaz de traduzir 15 000 000 mensagens simultaneamente, que o cérebro processa sem parar. Graças a isso, enxergamos o mundo com milhares de nuances coloridas. Escreva o número acima usando notação científica.
4 - Coloque na forma de Notação Científica:
a) 721 000 = b) 0,00000000023 = c) 0,0045 =
5 - Calcule o valor das expressões, simplificando quando possível:
Bons estudos! Professor Marcos
"E lembrem-se de sempre lavar bem as mãos e evitar sair de casa! Somente juntos, com a colaboração de todos, conseguiremos superar esta situação!"
E.M.A.C. Rodrigues Alves















2 Comentários
TEM O GABARITO DESSA ATIVIDADE?
ResponderExcluirNão
Excluir